子弹证明：一种区块链中的隐私保护技术

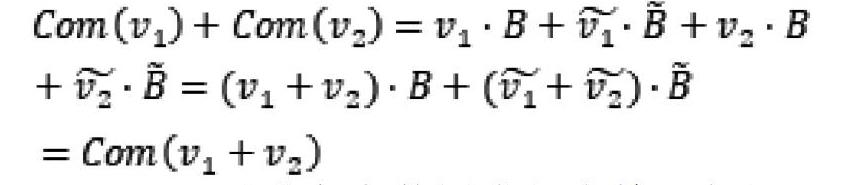
　　摘 要：区块链的隐私保护技术自2008年比特币问世以来就成为研究热点之一。加密货币如门罗币（Monero）、大零币（ZCash）、达世币（Dash）等都是成功应用各类隐私保护技术的明星货币，而在诸多的隐私保护技术之中，零知识证明技术能实现最好的匿名性，因此也成为隐私保护研究领域的焦点技术之一。论文对最新的子弹证明技术进行系统性和原理性的阐述分析，并与Zk-snarks和Zk-starks两类前沿零知识证明技术进行对比。最后，对区块链中的零知识证明技术的发展方向进行展望。

　　关键词：隐私保护；零知识证明；机密交易；子弹证明；范围证明

　　中图分类号：TP309.7 文献标识码：A

　　Abstract： The privacy-preserving technologies on blockchains have been well studied since the invention of Bitcoin in 2008. Monero， Z-cash， Dash are the well-known crypto-currencies for their advanced privacy-preserving technologies. Zero-knowledge proof which provides the best anonymity， is the hot-spot of the block chain privacy and security. This survey paper focuses on the introduction of the cutting-edge technique， i.e.， the bullet proofs with its underlying principles. We also make some remarks on the bullet-proofs， with the other two similar zero-knowledge proofs， Zk-snarks and Zk-stark. And we make the conclusion for the envision of the zero-knowledge proofs in the blockchain industry.

　　Key words： privacy-preserving； zero-knowledge proofs； confidential transactions； bullet proofs； range proofs

　　1 引言

　　區块链技术作为一种新兴的技术应用模式，主要解决了网络空间里交易的信任和安全问题。其核心思想是区块链里的每一个节点都按照块链式结构存储全局完整的账本数据，通过共识机制保证交易的有效性以及各节点存储的一致性。自从2008年比特币问世以来，其背后的核心区块链技术就持续蓬勃发展，从共识机制、点到点分布式网、智能合约，到上层的激励模型等多个方向都在不断衍变。经过十多年的发展，区块链技术已经在加密货币领域证明了其可靠性和安全性。

　　2 背景

　　区块链中的隐私保护问题，例如加密货币里的匿名交易、智能合约的隐私、区块链隐私保护基础设施等都是长期的研究热点。按隐私保护技术分类，零知识证明、安全多方计算、同态加密、环签名、代理重加密等，都是依靠密码学技术来实现对数据隐私的保护。而其中，零知识证明作为能实现最强匿名性的隐私保护技术，一直受到各区块链项目的重点研究和探索。

　　从应用的角度来看，区块链技术的各大应用场景，例如加密货币、电子存证、身份识别、金融数据结算等对隐私保护的要求也越来越高。其中，加密货币是目前为止区块链技术最为成功的应用，诞生了诸如门罗币（Monero）、大零币（ZCash）、达世币（Dash）等非常优秀的隐私货币。零知识证明，作为能实现最强匿名性的隐私保护技术，一直受到这些加密货币项目的重点研究和探索。

　　零知识证明[1]是由S.Goldwasser、S.Micali和C.Rackoff在20世纪80年代初提出的。它是一种证明者能使验证者相信某个论断是正确的，同时这个证明过程不泄露任何有用的信息。零知识证明属于交互式证明系统，除了传统的完备性和可靠性必须满足之外，其特有的零知识性保证了验证者在被证明过程中无法获得证明者拥有的秘密或者任何有助于获得该秘密的其他信息。长期以来，零知识证明作为一种强安全的隐私保护技术，在理论上获得了长足的研究和发展，但是其性能参数包括需要非常多的交互证明轮数、证明的数据长度、生成时间和验证时间，常常是制约该技术获得实际应用的瓶颈。

　　3 机密交易和范围证明

　　加密货币交易中的隐私性通常可以分为两类：一是匿名性，即交易双方的身份可以被隐藏起来；二是机密性，即该笔交易的交易金额是不可见的。早期的加密货币项目例如比特币，其交易由于没有把收款人和付款人的比特币地址与他们各自在真实世界中的身份信息进行关联，保证了一定程度的“弱匿名性”。因此，如何保证交易金额的机密性就成为了制约比特币和其他加密货币，以及各类区块链项目发展的一大限制。

　　3.1 机密交易

　　Maxwell在2016年[2]提出了“机密交易”（Confidential Transactions）的概念。注意，比特币等加密货币的交易形式称为未花费的交易输出（Unspent Transaction Outputs，UTXO），即当前这笔交易的其中一个输入使用的是之前某一笔交易的未使用过的一个输出，并且需要附加当前交易输入地址对应的数字签名。因此，UTXO模式的交易验证的主要思想是：验证当前交易的每一个输入都是属于UTXO，并且所有的输入总和大于所有的输出总和。机密交易的思想就是交易金额，即 UTXO形式交易中的各个输入和输出，用承诺算法隐藏起来；同时，为了支持公开可验证性（否则失去了区块链的透明和可审计的意义），机密交易还会包含一段零知识证明，用来证明交易的输入总和大于输出总和，并且所有的输出都是正值。

　　在机密交易中，交易金额通常用Pedersen承诺算法[3]隐藏起来。该承诺算法主要是承诺者先向接收者承诺某个秘密数，即生成某个承诺值，在后面的阶段通过展示该秘密数，由接收者确认前后承诺值是否相等。注意，承诺算法的两个要求：一是隐藏性（Hiding Property），即承诺值不能泄露任何关于秘密数的信息；二是绑定性（Binding Property），即承诺者给出承诺值后，无法更换承诺中的秘密数，使得在后面的阶段用新的秘密数生成相同的承诺值，从而欺骗接收者。

　　基于椭圆曲线的Pedersen承诺算法主要形式如下：

　　Com（v）=v·B+·這里B和分别是作为公开参数的生成元，为椭圆曲线上的两个基点，v是需要承诺的秘密数，是一个盲化因子， 用来保证语义安全性。

　　Pedersen承诺方案不但满足承诺方案的两个传统的安全要求，完美的隐藏性（Perfect Hiding Property），和计算绑定性（Computationally Binding Property），而且具备非常好的同态加密性（Homomorphic Encryption），即：

　　Pedersen承诺方案的同态加密性，保证了UTXO交易中多个输入和多个输出的总和均是Pedersen承诺，即交易金额数可隐藏。

　　3.2 范围证明

　　为了“零知识”地证明机密交易中的输入和大于输出和，需要依赖一种称之为“范围证明”[4]的技术。范围证明主要是证明经过加密或者承诺等隐藏处理之后的某个秘密数，其取值在某一个特定区间内。

　　大多数的范围证明方案看上去非常适合成为机密交易的一个组成部分，但是它的主要缺点在于需要一个可信任的初始化阶段，以及时间和空间上带来的巨大性能开销。依赖初始化阶段的可信环境，会给该区块链的透明性带来质疑。采用了范围证明的机密交易开始，会变得非常大而且验证缓慢，其中的一个范围证明大小约为几千个字节，且需要几个毫秒才能验证。而传统的UTXO交易里的数字签名小于100个字节，且验证时间不超过100微秒。因此如果能解决这两个问题，那么机密交易看起来就能真正成为可能。

　　4 子弹证明原理

　　子弹证明是2017年由Bunz等人[5]提出的一种非交互式零知识证明，用于解决机密交易中证明技术的可信启动问题和性能问题。相比于文献[5]，用加法群代替了原先的乘法群符号系统，同时将原文献的证明推导过程以更详细的公式和文字进行表述。

　　4.1 符号系统

　　用如下的符号定义系统。小写字母a、b、c表示Zp里的标量，大写字母G、H、P、Q表示群G里的元素。向量被记为粗体，例如a和G。而两个向量的内积记为<-，->。请注意内积∈Zp输出的是一个标量，而内积∈G是一个多标量的乘法。 全0和全1的向量记为0，1。对一个标量y，用

　　表示相关的一个向量，且第i个元素是yi。对于具有偶数长度2k的向量v，定义分布为该向量的低半段和高半段：

　　Pedersen承诺方案被记为：

　　并且B和是这里被使用到的生成元和“盲化”因子（Blinding Factors），将v的盲化因子记为，使得变量和它的盲化因子之间可以清晰地关联起来。为方便起见，用Com（v）符号代替Com（v·）。

　　同时，也用到了Pedersen向量承诺方案，定义为：

　　且G和H都是生成元组成的向量。

　　顾名思义，范围证明是“零知识地”去证明一个数值在某一个区间范围内。证明者将要证明的值v，先进行承诺V=Com（v）发送V给验证者。证明者希望在接下来的过程里能证明v∈[0，2n），同时不泄露v的具体的值。假设a是v的各个比特位组成的向量，例如n=3，v=7，a就是<1，1，1>；n=4，v=10，a就是<0，1，0，1>。v可以被表示成一个内积，即：

　　必须保证a是一个只包含{0，1}的向量。这也可以用另一种形式来表示：

　　且x○y记为两个向量之间的元素积。

　　因此二进制表示v时，v∈[0，2n）等价于以下两个等式：

　　更进一步，其实关注的是向量a和a-1， 因此记aL=a，aR=a-1从而获得

　　4.2 合并多向量陈述证明

　　接下来需要对这三个等式进一步处理，使之合并转化为一个式子（statement），方便证明。因为b=0当且仅当=0对于任意的y。因此上述三个等式可以转化为

　　对于验证者选择任意的y都成立。

　　更进一步地，对于验证者任意选择的y，都可以有：

　　4.3 合并内积

　　需要再将上面等式里的这些项进一步处理，转化成一个内积的形式，且转化后的内积<-，->里，aL只出现在左边，aR只出现在右边，且将不包含秘密数的那些项合并起来记为一个新变量δ。

　　将这个陈述拆开，再重新排列之后，两边同时加上<-z1，z22n+zyn>之后再约简。将所有的非秘密项整理到内积之外，记为：

　　最后获得了等式：

　　将内积地左边部分记为“unblinded l（x）”，右边部分记为“unblinded r（x）”，因此有：

　　4.4 内积盲化

　　证明者不能简单地将“unblinded l（x）”和“unblinded r（x）”直接发送给验证者，这样将会导致证明过程不是“零知识化”。因此，聪明的证明者会随机地选取这两个向量的盲化因子：

　　sl，sr←Zpn并且用他们来构造盲化后的多项式：

　　l（x）和r（x）将项al，ar盲化，用项aL+sLx，aR+sRx代替。其中，l0和r0项表示多项式里度数为0的项（关于x），类似的l1和r1表示多项式里度数为1的项。

　　很显然，有：

　　然后记：

　　将系数t（x）用 Karatsuba方法展开：

　　因为：

　　证明者希望对验证者证明上面那个未盲化的内积等式成立，实质上等价于证明：1. t（x）的常数项t0等于z2v+δ（y，z）， 并且 2. t（x）是正确的多项式。证明t（x）是正确的多项式，等价于证明l（x）， r（x）均是正确的，并且t（x）=。

　　4.5 证明t0的正确性

　　证明者首先制作一个关于t（x）的系数的承诺，然后将通过准确回答验证者给出的任意挑战值，来向验证者证明“这些承诺是对t（x）的正确承诺”。 证明者已经用V=com（v）来承诺了v（本质是承诺了t0），因此证明者再计算两个承诺：T1=com（t1） 和T2=com（t2），并且把这些承诺发送给了验证者。注意到，这些承诺互相之间且与均形成了一些关系，即我们有如下的式子：

　　请注意每个列的和是一个对该列第一行里的变量承诺，且该承诺用了该列第二行里的变量作为盲化因子。而所有列的和就是， 即对 在取值时进行承诺， 且用了正交盲化因子：

　　为了向验证者证明，证明者将向验证者发送，后者根据以下式子检查一致性：

　　4.6 证明的正确性

　　希望将和与，和这一组变量进行关联。因为有：

　　需要找到关于和这两个复合变量的承诺。但是知道证明者必须在验证者给出挑战值y之前计算出承诺，因此证明者只具备对和计算对应的承诺值的能力。验证者需要将证明者的承诺变形成 （对也要进行类似的变形）。 注意到：

　　因此记， 则关于的承诺被变形为关于的承诺。

　　为了将证明者的承诺和承诺关联到和，用到如下式子：

　　其中。

　　与前面那个和式对列与行的分析类似，不难发现，上面式子里的每一列都是一个Pedersen向量承诺，且第三行里的元素均是相应的盲化因子。所有列的和，也是一个Pedersen向量承诺，其正交盲化因子是。为了向验证者证明，证明者需要将发送给验证者，后者计算以下的式子：

　　如果证明者是诚实的，则，因此验证者用作为内积协议的输入来证明。

　　4.7 内积协议

　　首先，一个直接的办法是证明者将向量and直接发送给验证者，后者可以根据以下式子直接计算内积和承诺是否是正确的。

　　尽管这样做不会造成信息泄露，即证明过程确实是零知识化，但是需要在证明者和验证者之间传递个标量。为了节省带宽，给出内积论证协议（inner-product argument protocol），可以进行间接地证明，并且通信开销减低到。

　　接下来需要修改一下符号定义系统，使得这部分将要阐述的內积协议的定义不会与前文的范围证明的定义冲突：

　　根据这套新的定义，需要进行以下这一个知识证明：

　　引入一个中间变量，再对第二个等式两侧同时乘以一个正交生成元，将这两个等式合并为一个等式，即：

　　继续引入以下符号对上面地等式简化：

　　将获得：

　　上面这个合并后的等式非常关键，因为它可以对等式里的各个向量进行持续地“对半压缩”并且压缩后获得的新等式仍然保持相同的结构。通过压缩次，会获得一个最终等式只有2个向量且每个向量的长度只包含有一个元素，这样最后的校验就变得非常简单。需要强调的是，这里如果证明了对于所有的，都有上述等式里的组成结构，那么上面的和也一定会符合等式。在UTXO模型里，只要证明交易的输入大于输出，这笔交易就可以被认为是有效的。也就是输出在0和输入之间。接下来介绍一下具体压缩的过程。引入一个中间变量，并且对原始的进行如下变换：

　　令，并且采用与类似的结构，但是用的是压缩后的向量来定义：

　　将它展开得到：

　　然后我们将这个等式进一步表示成如下这个等式：

　　如果证明者确实是诚实地在随机选择之前对和进行了承诺计算，并且上面这个等式成立，则原始的等式（关于的那个等式）是极大概率成立。接下来可以继续对压缩，与上面过程类似地引入中间变量，...，一直到到达最后的我们有：

　　将上面的等式按照定义和，进行重写后发现：

　　到这一步，证明者可以简单地发送2个标量和给验证者，这样后者可以直接校验上面这个最终步的等式是否成立。总体的内积协议有步，并且每一步都需要证明者将发送给验证者，。至此，对于证明，的正确性，一共需要发送个元素。

　　至此，阐述了一个交互式地给出高效的范围证明。通过采用Fiat-Shamir技术[6]将上述证明过程转化为非交互式，就能获得真正意义上的一个子弹证明。事实上，子弹证明的另外一大优点是在整合处理的高效性。将多个机密交易的子弹证明整合/合并为一个子弹证明，增加的字节数非常的少（仅以对数级增长）。

　　4.8 子弹证明，Zk-snarks和Zk-starks

　　除了Bulletproofs之外，Zk-snarks和Zk-starks也是非常适合隐藏交易细节的零知识证明技术。

　　Zk-snarks技术[7]允许将任何复杂的验证问题转化为一个多项式验证问题，再利用椭圆曲线上的指数知识困难假设[8]和同态隐藏手段，以及Fait-Shamir转换技术，获得最终形式的一种简洁且非交互式的零知识证明。Zk-snarks目前主要应用于大零币（Zcash）的隐私交易里。但是，Zk-snarks的主要缺点在于它的安全性完全依赖于一个可信启动（Trusted Setup），即证明系统的内建随机参数初始化必须保证不能被任何人掌握，需要通过一些特殊的密码学技术如（Shamir秘密分割[9]）来达成。

　　Zk-starks[10]是Zk-snarks的“变种”技术，主要解决了Zk-snarks的可信启动问题，同时引入了更加简单的密码学困难假设，能抵抗量子攻击。但产生的问题是，一个Zk-snarks证明的大小将达到几百千字节（KB），这让Zk-starks的实际应用再次受限。

　　虽然不能简单地总结这三种引领加密货币隐私防护的零知识证明技术，孰优孰劣，甚至在具体的性能方面，也很难简单地给出比较。但是，可以确定的是，子弹证明技术不依赖可信启动，比Zk-snarks和Zk-starks有相对更短的证明长度，以及支持快速批处理的优势，将会在很多区块链领域特定的隐私保护场景里找到一席之地。

　　5 结束语

　　随着隐私货币门罗币（Monero）开始采用子弹证明作为其最新的匿名交易技术，门罗币的环加密交易（一种以环签名的形式保护交易匿名性的技术）效率明显地提高，且交易大小的增长由原先的线性变为对数性，提高了隐私性以及可扩展性。而Zk-snarks已经是隐私货币大零币（ZCash）最重要的隐私保护手段之一，此外该货币也在考虑采用Zk-starks证明技术。可以看到这些优秀的零知识证明技术在加密货币领域已经得到了实践性的应用和发展。在未来，不仅限于子弹证明，各类零知识证明技术将会更加广泛和可靠地为公有链、联盟链的应用场景提供隐私保护。

　　参考文献

　　[1] Goldwasser S， Micali S， Rackoff C. “The knowledge complexity of interactive proof systems[J]， SIAM Journal on Computing， Philadelphia： Society for Industrial and Applied Mathematics， 18 （1）： 186–208， doi：10.1137/0218012， ISSN 1095-7111.

　　[2] Maxwell， G. Confidential transactions. https：//people.xiph.org/～greg/ confidential_values.txt， 2016.

　　[3] Pedersen TP. Non-interactive and information-theoretic secure verifiable secret sharing[M]. Advances in Cryptology CRYPTO ‘91 Springer 1991.

　　[4] Bootle J， Cerulli A， Chaidos P， Groth J， Petit C. Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting[C]. In Annual International Conference on the Theory and Applications of Cryptographic Techniques， pages 327–357. Springer， 2016.

　　[5] Bunz B， Bootle J， Boneh D， Poelstra A， Wuille P， Maxwel l G. Bulletproofs： short proofs for confidential transactions and more[C]. IEEE Symposium on Security and Privacy， 2018， pp.315-334.

　　[6] Fiat A， Shamir A. How to prove yourself： practical solutions to identification and signature problems[J]. CRYPTO 1986： pp. 186-194.

　　[7] Ben-Sasson E， Chiesa A， Tromer E， Virza M. Succinct non-interactive zero knowledge for a von Neumann architecture[C]. Proceedings of the 23rd USENIX conference on Security Symposium. Pages 781-796.

　　[8] Bellare M， Palacio A. The knowledge-of-exponent assumptions and 3-round zero-knowledge protocols[J]. Cryptology eprint archive. https：//eprint.iacr.org/2004/008.pdf.

　　[9] Shamir Adi. How to share a secret[J]. Communications of the ACM. 1979. 22 （11）： 612–613.

　　[10] Ben-Sasson E， Bentov I， Horesh Y， Riabze M. Scalable， transparent， and post-quantum secure computational integrity[J]. Cryptology eprint archive. https：//eprint.iacr.org/2018/046.pdf.

　　作者簡介：

　　夏伏彪（1985-），男，汉族，浙江宁波人，英国伯明翰大学，博士；主要研究方向和关注领域：应用密码学、区块链技术。

　　高庆忠（1974-），男，汉族，福建漳州人，上海交通大学，硕士；主要研究方向和关注领域：区块链和人工智能技术。

　　刘军（1981-），男，汉族，江西吉安人，上海交通大学，硕士；主要研究方向和关注领域：区块链、人工智能和大数据分析。

　　林锦达（1985-），男，汉族，福建漳州人，中国科学院大学，博士；主要研究方向和关注领域：人工智能、数据分析、区块链技术。

　　夏伏彪　高庆忠　刘军　林锦达